2023年初中数学反比例函数中的“面积模型”

一、反比例函数中的“面积模型”

反比例函数是“自带”“面积模型”的！

常言：“龙生龙，凤生凤”，发比例函数一旦诞生，就“自带”贵族气质——“自带”“面积模型”。反比例函数就是这么“任性”！

   （一）反比例函数图像上的坐标矩形与坐标三角形的面积（以下部分内容选自《沙场秋点兵》）

1、如图1，若反比例函数解析式为y=x/k，则；S矩形OBAC=|k|；

2、如图2，若反比例函数解析式为y=x/k，则；S△OAB=1/2·|k|。

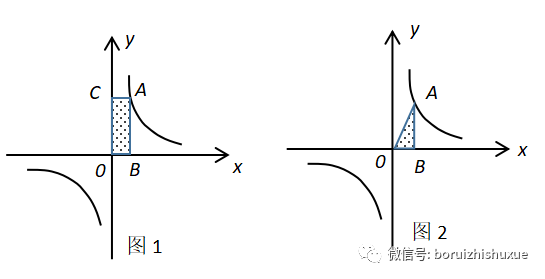
    关于这两个结论的证明，自然不用赘述，关于这两个结论的灵活应用，则更是仪态万千，手头有《沙场秋点兵》的话，上面有许多练习，自己练练。也可从本公众号找到去年推送的文章——反比例函数中的面积问题》自己打印练习......

（二）反比例函数中的三角形与等积梯形

1、如图3，若反比例函数解析式为y=k/x，则；S△OAB=S梯形BCDA；

2、如图4，若反比例函数解析式为y=k/x，则（1）S△OAB=S梯形CDEA；（2）

 CD²=EB·EA；

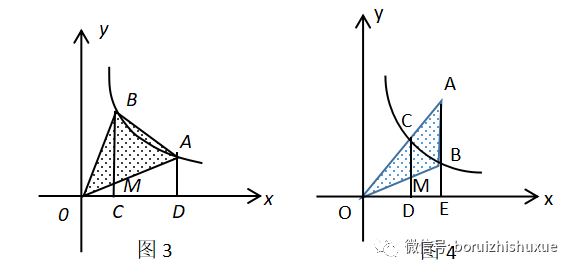
这两个结论，其实是前面结论的更进一步，但是，已经有些同学不太好理解了。其证明如下：

1、如图3，易知S_△BOC=S_△AOD=1/2·|k|，∴S_△AOM=S_梯形ADCM，∴S_△BOM+S_△ABM=S_梯形ADCM+S_△ABM，即S_△AOB=S_梯形BCDA；

2、如图4，易知S_△COD=S_△BOE=1/2·|k|，∴S_△COM=S_梯形BEDM，则（1）S_△COM+S_{△梯形ABMC}=S_梯形BEDM+S_梯形ABMC，即S_△AOB=S_梯形BEDM；（2）易知CD·OD=BE·OE，∴BE:CD=OD:OE=CD:AE，即CD²=EB·EA。

（三）过双曲线上两点的矩形或直角三角形

如图5：

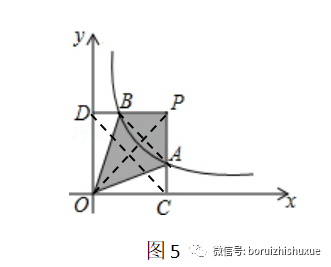
1、S_△OAP=S_△OPB=1/2(S_矩形OCPD-|k|）；

2、（1）PB：BD=PA：AC；（2）AB∥CD；

这两个结论的证明不算太难：

1、∵矩形PCOD，∴△PCO≌△PDO，则S_△PCO=S_△PDO，由（一）知，S_△ACO=S_△BDO=1/2·|k|，∴S_△OAP=S_△OPB=1/2(S_矩形OCPD-|k|）；

2、∵S_△ACO=S_△BDO，S_△OAP=S_△OBP，∴PB·OD=PA·OC，BD·OD=AC·OC；∴PB：PA=AC：BD=OC:AD，则PB:BD=PA:AC，∴AB∥CD；