2023年初中数学“面积法”在建立反比例函数线段模型中的作用

“面积法”在建立反比例函数线段模型中的作用

“面积法”是一个古老而又新兴的话题，从古老的“勾股定理”的证明，到现在的计算机证明，“面积法”有时候起着化腐朽为神奇的绝妙作用。有些题目，用常规解法比较麻烦，而用“面积法”则简洁明了。简单的来说：运用面积公式、面积之间的和差关系、积的不变性等来解决问题的方法统称为面积法（若有时间，再单独探讨）。在解决反比例函数的相关问题时，灵活运用“面积法”，也能得出一些常见的线段基本模型。

（一）同一象限内反比例函数图像上两点连线的平行线

1、如图6，过反比例函数y=k/x上两点A、B，分别作坐标轴的垂线 ，垂足为C、D，则AB∥CD；

2、如图7，过反比例函数y=k/x图像上的点A、B分别向两条坐标轴作垂线，垂足分别为E、F、C、D，则AB∥CD∥EF；

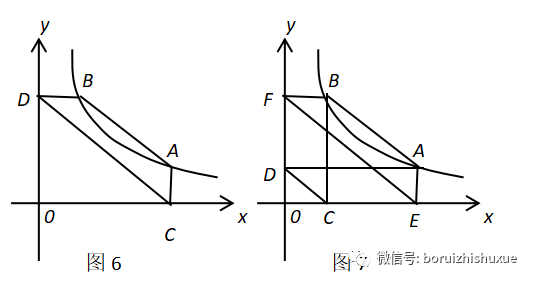
对于1中的结论，可以仿照图5中2的证法。也可以在图7中，一次性予以证明。我们从证明中可以体会到“面积法”的神奇作用。

如图8，连接AF、BE、AC、BD，则S_△ADC=S_△BCD=1/2·|k|，∴AD·CM=BC·DM，即AD:DM=BC:CM，则AB∥CD；且易知∴S_△BEF=S_△AEF=1/2·|k|，根据等底等高的三角形面积相等，则△BEF和△AEFEF边上的高相等，则AB∥EF。∴AB∥CD∥EF。

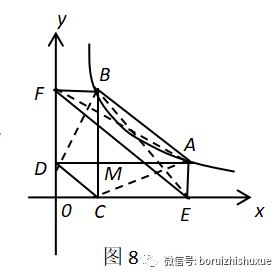
    根据这里两个结论，我们进而可以得到下面的结论：

    （二）一次函数被反比例函数所截得到的等线段

1、如图9，若一次函数y=k₁x+b与反比例函数y=k₂/x交于点A、B，与坐标轴交于点C、D，则AC=BD；

2、如图10，若一次函数y=k₁x+b与反比例函数y=k₂/x交于点A、B，与坐标轴交于C、D，则AC=BD；

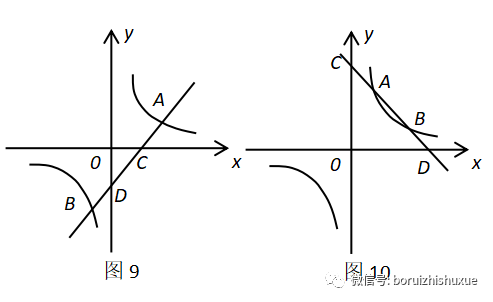
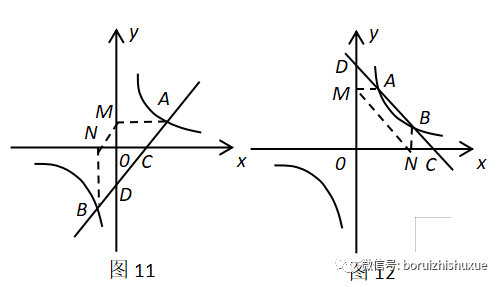
如图11、图12，分别过点A、B作AM⊥y轴于点M，BN⊥x轴于点N，连接MN。运用面积法，仿照（一）中的证明方法，易证明MN∥AB，则易证明四边形BDMN和四边形ACNM是平行四边形，∴在图11中，AC=MN=BD。在图12中，AM=NC，DM=BN，则易证△ADM≌△CBN，则AD=BC。