一栋高楼上安放了一块高约10米的LED广告屏，一测量爱好者在与高楼底部同一水平线上的C处测得广告屏顶端A处的仰角为31.80°．再向大楼前进20米到D处，测得广告屏顶端A处的仰角为37.38°（人

问题描述：

一栋高楼上安放了一块高约10米的LED广告屏，一测量爱好者在与高楼底部同一水平线上的C处测得广告屏顶端A处的仰角为31.80°．再向大楼前进20米到D处，测得广告屏顶端A处的仰角为37.38°（人的高度忽略不计）．
（1）求大楼的高度（从地面到广告屏顶端）（精确到1米）；
（2）若大楼的前方是一片公园空地，空地上可以安放一些长椅，为使坐在其中一个长椅上观看广告屏最清晰（长椅的高度忽略不计），长椅需安置在距大楼底部E处多远？已知视角∠AMB（M为观测者的位置，B为广告屏底部）越大，观看得越清晰．

---

最佳答案：

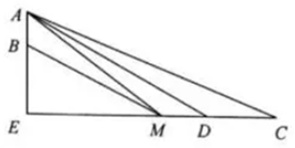（1）由题意，∠ACD=31.80°，∠ADE=37.78°，
∠CAD=5.98°，CD=20，
由正弦定理可得AD=

CDsin∠ACD

sin∠CAD

≈101.2，
∴AE=ADsin∠ADE≈62m；
（2）设∠AMB=α，α∈(0，

π

2

)，EM=x，x>0，
tan∠AME=

62

x

，tan∠AME=

52

x

，
tanα=tan（∠AME-∠BME）=

10x

x2+3224

=

10

x+ 3224 x

≤

10

4 806

当且仅当x=

3224

≈57m时，tanα取得最大值，此时α也最大．