如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”，已知点A、B、C、D分别是“果圆”与坐标轴的交点，AB为半圆的直径，抛物线的解析式为y=x2-2x-3，求这个“果圆”被y轴
问题描述：
如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”，已知点A、B、C、D分别是“果圆”与坐标轴的交点，AB为半圆的直径，抛物线的解析式为y=x2-2x-3，求这个“果圆”被y轴截得线段CD的长___．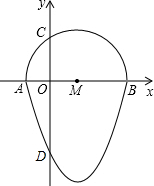
最佳答案：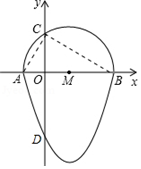 
连接AC，BC．
∵抛物线的解析式为y=x2-2x-3，
∴点D的坐标为（0，-3），
∴OD的长为3．
设y=0，则0=x2-2x-3，解得：x=-1或3，
∴A（-1，0），B（3，0）．
∴AO=1，BO=3，AB=4，M（1，0）．
∴MC=2，OM=1．
在Rt△COB中，OC=
| CM2-OM2 |
| 3 |
∴CD=CO+OD=3+
| 3 |
| 3 |
故答案为：3+
| 3 |
版权声明
声明：有的资源均来自网络转载，版权归原作者所有，如有侵犯到您的权益
请联系本站我们将配合处理！