如图所示，传送装置由轮半径均为R=1π米的主动轮O2和动轮O1以及始终绷紧的传送带等构成，装置倾角θ=30°，上下两轮轴心O1、O2相距L=10m，A、B两点为传送带与转动轮的相切点．现将一煤块（

问题描述：

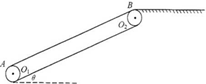
如图所示，传送装置由轮半径均为R=

1

π

米的主动轮O₂和动轮O₁以及始终绷紧的传送带等构成，装置倾角θ=30°，上下两轮轴心O₁、O₂相距L=10m，A、B两点为传送带与转动轮的相切点．现将一煤块（可视为质点）轻放在传送带的A点，经传送带向上传送，在B点进入上平台．已知煤块与传送带之间的动摩擦因数μ=

3

2

，g取10m/s²． （1）若传送带始终以v=5m/s的速率顺时针转动，则煤块从A到B所用的时间为多少？（2）要想尽快将煤块由A点运送到B点，则传送带的速率至少应为多大？（3）煤块与传送带相对滑动时会在传送带上留下黑色的痕迹，那么，当传送带的速率满足什么条件时，能使传送带上留下的黑色痕迹最长？

---

最佳答案：

（1）煤块从A到B过程，先加速后运动，由牛顿第二定律得：μmgcosθ-mgsinθ=ma，代入数据解得：a=2.5m/s2，煤块加速的时间为：t1=

v

a

=

5

2.5

=2s，加速位移为：x1=

v2

2a

=

52

2×2.5

=5m，匀速运动的时间为：t2=

L-x1

v

=

10-5

5

=1s，从A到B煤块的运动时间为：t=t1+t2=3s；（2）要使煤块尽快由A运动到B点，煤块应一直加速运动，由v22=2aL，代入数据解得：v2=5

2

m/s≈7.07m/s，则传送带的速率至少为7.07m/s；（3）传送带的速度越大，黑色痕迹越长，黑色痕迹最长为传送带的长度，即：s=2L+2πR，s=22m，煤块由A点运送到B点时间内，传送带运转的距离：s总=s+L，s总=32m，煤块由A到B的运动时间为：t3=

v

a

，解得：t3=2

2

s，传送带运转的速度至少为：v3=

s总

t3

，解得：v3=8

2

m/s≈11.3m/s，则初速度的速率大于11.3m/s时，能使传送带上流向的黑色痕迹最长；答：（1）若传送带始终以v=5m/s的速率顺时针转动，则煤块从A到B所用的时间为3s；（2）要想尽快将煤块由A点运送到B点，则传送带的速率至少应为7.07m/s；（3）当传送带的速率v≥11.3m/s时，能使传送带上留下的黑色痕迹最长．