三角形中位线定理的证明方法

三角形中位线定理是三角形的中位线平行于第三边（不与中位线接触），并且等于第三边的一半。

证明方法

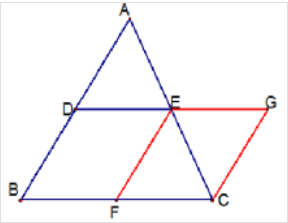
已知△ABC中，D，E分别是AB，AC两边中点。求证DE平行于BC且等于BC/2

过C作AB的平行线交DE的延长线于G点。

∵CG‖AD

∴∠A=∠ACG

∵∠AED=∠CEG、AE=CE、∠A=∠ACG(用大括号)

∴△ADE≌△CGE (A.S.A)

∴AD=CG(全等三角形对应边相等)

∵D为AB中点

∴AD=BD

∴BD=CG

又∵BD‖CG

∴BCGD是平行四边形(一组对边平行且相等的四边形是平行四边形)

∴DG‖BC且DG=BC

∴DE=DG/2=BC/2

∴三角形的中位线定理成立。

外角平分线定理证明方法

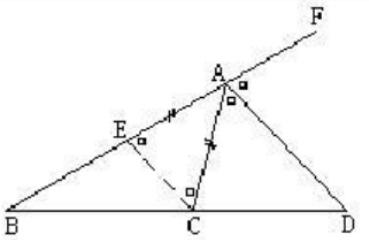
如图，AD是△ABC中∠BAC的外角∠CAF的平分线。求证：BA/AC=BD/DC

证明：过C作CE‖DA与BA交于E。则：BA/AE=BD/DC

∵∠DAF=∠CEA；∠DAC=∠ECA；∠DAF=∠DAC。

∴∠CEA=∠ECA；∴AE=AC；∴BA/AC=BD/DC。