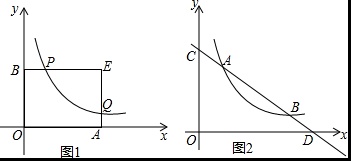
阅读理如图1,点P,Q是双曲线上不同的两点,过点P,Q分别作PB⊥y轴于B点、QA⊥x轴于A点,两垂线的交点为E点,则有PEPB=QEQA,请利用这一性质解决问题
问题描述:
阅读理 如图1,点P,Q是双曲线上不同的两点,过点P,Q分别作PB⊥y轴于B点、QA⊥x轴于A点,两垂线的交点为E点,则有| PE |
| PB |
| QE |
| QA |
问题解决:
(1)如图1,如果QE=6,AQ=3,BP=4.填空:PE=___;
(2)如图2,点A,B是双曲线y=
| k |
| x |
①求证:AC=BD.
②已知:直线AB的关系为y=-x+2,CD=4AB.试求出k的值.
 最佳答案:
最佳答案: (1) ∵PEPB=QEQA,QE=6,AQ=3,BP=4,∴PE=PB?QEQA=4×63=8.故答案为:8.(2)①证明:过点A作y轴的垂线交y轴于点E,过点B作x轴的垂线交x轴于点F,延长EA、FB交于点M,如图3所示.∵ME⊥y轴,MF⊥x轴,∴△CAE...
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
