在平面直角坐标系xOy中，圆C的方程为x2+y2﹣8x+15=0，若直线y=kx﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值是______
在平面直角坐标系xOy中，圆C的方程为x2+y2﹣8x+15=0，若直线y=kx﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值是______
【答案】
∵圆C的方程为x2+y2﹣8x+15=0，整理得：（x﹣4）2+y2=1，即圆C是以（4，0）为圆心，1为半径的圆；
又直线y=kx﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，
∴只需圆C′：（x﹣4）2+y2=1与直线y=kx﹣2有公共点即可．
设圆心C（4，0）到直线y=kx﹣2的距离为d，
则d=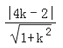
≤2，即3k2﹣4k≤0，
∴0≤k≤
．
∴k的最大值是 ．
所以答案是： ．
版权声明
声明：有的资源均来自网络转载，版权归原作者所有，如有侵犯到您的权益
请联系本站我们将配合处理！