2023年初中数学-相似三角形

之前，我们介绍过全等三角形，因为全等三角形的情况还是太特殊了，要求两个三角形完全相同，所以应用场景不多。

如果两个三角形大小成比例呢?是不是也可以算小的就能得知大的了?这里有个著名的故事：

那时候，人们建造了高大的金字塔，可是谁也不知道金字塔究竟有多高。有人说：“要想测量金字塔的高度，比登天还难!”这话传到欧几里得耳朵里。他笑着告诉别人：“这有什么难的呢?当你的影子跟你的身体一样长的时候，你去量一下金字塔的影子有多长，那长度便等于金字塔的高度!”

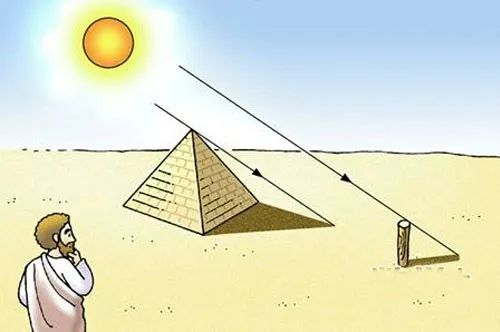
欧几里得利用相似三角形算高度

这就是我们学习相似三角形的价值，其实“等比例放缩”的思想很重要。生活中有大量问题，都可以通过等比例放缩来变得可以计算。

1.相似三角形的定义

三个对应的内角的角度都一样(但边长大小不需一样)的两个三角形，或：对应角相等，对应边成比例的两个三角形称为“相似三角形(similar triangles)”，其对应边之比称为相似比;两个相似比为1的相似三角形称为全等三角形。

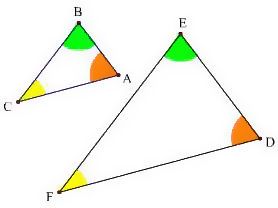
相似三角形

2.性质

2.1.若两个三角形相似，则三个对应角相等。

∠A=∠D,∠B=∠E,∠C=∠F

2.2.若两个三角形相似，则三个边的边长对应成比例。

除此之外，两三角形对应的中线、高、角平分线、周长均成比例，面积比是相似比的平方。

3.判定方法

3.1.两个角对应相等的三角形相似

3.2.两条边成比例，其夹角又相等的两个三角形相似

3.3.三边成比例的两个三角形相似

3.4.两个直角三角形的斜边、直角边成比例则相似