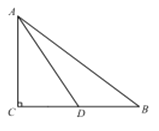
如图,在Rt△ABC中,∠C=90°,点D是BC边的中点,BD=2,tanB=<img alt="1" src="/tk/20210512/162076839447
如图,在Rt△ABC中,∠C=90°,点D是BC边的中点,BD=2,tanB=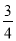 .
.
(1)求AD和AB的长;
(2)求sin∠BAD的值.
(1)AB=5,AD=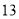 ;(2)
;(2)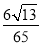 .
.
(1)由中点定义求BC=4,根据tanB=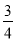 得:AC=3,由勾股定理得:AB=5,AD=
得:AC=3,由勾股定理得:AB=5,AD=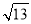 ;
;
(2)作高线DE,证明△DEB∽△ACB,求DE的长,再利用三角函数定义求结果.
(1)∵D是BC的中点,CD=2,
∴BD=DC=2,BC=4,
在Rt△ACB中,由tanB=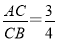 ,
,
∴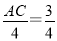 ,
,
∴AC=3,
由勾股定理得:AD=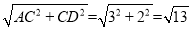 ,
,
AB=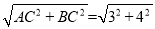 =5;
=5;
(2)过点D作DE⊥AB于E,
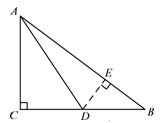
∴∠C=∠DEB=90°,
又∠B=∠B,
∴△DEB∽△ACB,
∴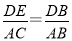 ,
,
∴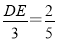 ,
,
∴DE=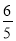 ,
,
∴sin∠BAD=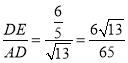 .
.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
