已知函数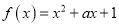
(Ⅰ)设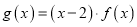 ,若
,若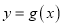 的图象与x轴恰有两个不同的交点,求实数a的取值集合.
的图象与x轴恰有两个不同的交点,求实数a的取值集合.
(Ⅱ)求函数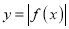 在区间
在区间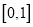 上的最大值.
上的最大值.
(Ⅰ)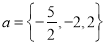 ;(Ⅱ)ymax=
;(Ⅱ)ymax=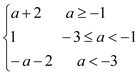
(Ⅰ)分类讨论,由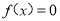 恰有一解及
恰有一解及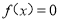 有两个不同的解求得;
有两个不同的解求得;
(Ⅱ)分类讨论,从而确定二次函数的单调性及最值,从而确定函数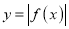 在
在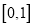 上的最大值.
上的最大值.
(Ⅰ)由题意得:
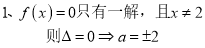
2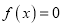 有两个不同的解,且其中一解x=2;
有两个不同的解,且其中一解x=2;
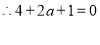
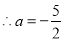
综上所述: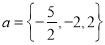
(Ⅱ)(1)若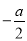 ≤0,即a≥0时,
≤0,即a≥0时,
函数y=|f(x)|在[0,1]上单调递增,
故ymax=f(1)=2+a;
(2)若0<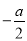 <1,即-2<a<0时,
<1,即-2<a<0时,
此时△=a2-4<0,且f(x)的图象的对称轴在(0,1)上,且开口向上;
故ymax=max{f(0),f(1)}=max{1,a+2}=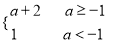
(3)若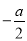 ≥1,即a≤-2时,
≥1,即a≤-2时,
此时f(1)=2+a≤0,
ymax=max{f(0),-f(1)}=max{1,-a-2}=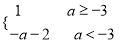
综上所述,ymax=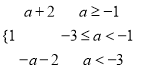
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
